1.
PENGERTIAN TREE
Kumpulan node yang
saling terhubung satu sama lain dalam suatu kesatuan yang
membentuk layakya
struktur sebuah pohon. Struktur pohon adalah suatu cara
merepresentasikan
suatu struktur hirarki (one-to-many) secara grafis yang mirip
sebuah pohon,
walaupun pohon tersebut hanya tampak sebagai kumpulan node-node
dari atas ke bawah. Suatu struktur data yang tidak linier yang
menggambarkan
hubungan yang hirarkis (one-to-many) dan tidak linier antara
elemen-elemennya.
Deklarasi Pohon
Jika kita
memperhatikan setiap simpul dalam pohon biner, kita bisa menyusun
struktur data yang tepat dari simpul-simpul tersebut. Kita dapat melihat
bahwa dalam setiap simpul selalu berisi dua buah pointer untuk menunjuk
ke cabang kiri dan cabang kanan, dan informasi yang akan disimpan
dalamsimpul tersebut. Dengan memperhatikan hal ini, simpul dalam pohon biner
disajikan sebagai berikut:

Sesuai dengan gambar 7.1, maka deklarasi list yang sesuai adalah:
typedef char TypeInfo;
typedef struct Simpul
*Tree;
struct Simpul {
TypeInfo Info;
tree Kiri, /* cabang
kiri */
Kanan; /* cabang kanan
*/
};
|
ISTILAH DALAM TREE

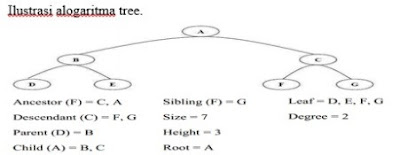
JENIS-JENIS TREE BINARY TREE
Tree dengan syarat
bahwa tiap node hanya boleh memiliki maksimal dua sub
pohon dan kedua
subpohon harus terpisah.
Kelebihan struktur
Binary Tree :
- Mudah dalam
penyusunan algoritma sorting
- Searching data
relatif cepat
- Fleksibel dalam
penambahan dan penghapusan data



KUNJUNGAN PADA POHON BINER
Sebuah pohon biner
memiliki operasi traversal yaitu suatu kunjungan pada
suatu simpul tepat
satu kali. Dengan melakukan kunjungan lengkap kita akan
memperoleh urutan
informasi secara linier yang tersinpan di dalam pohon biner.
Terdapat tiga
jenis kunjungan pada pohon biner, yaitu :
PREORDER
Kunjungan jenis
ini mempunyai urutan kunjungan sebagai berikut :
– Cetak isi
simpul yang dikunjungi.
– Kunjungi
cabang kiri.
– Kunjungi
cabang kanan.
Prosedur untuk
melakukan traversal secara PREORDER adalah sebagai berikut:

INORDER
Kunjungan jenis
ini mempunyai urutan kunjungan sebagai berikut :
– Kunjungi
cabang kiri.
– Cetak isi
simpul yang dikunjungi.
– Kunjungi
cabang kanan.
Prosedur untuk
melakukan traversal secara INORDER adalah sebagai berikut:

POSTORDER
Kunjungan jenis
ini mempunyai urutan kunjungan sebagai berikut :
– Kunjungi
cabang kiri.
– Kunjungi
cabang kanan.
– Cetak isi
simpul yang dikunjungi
Contoh Program:
|
#include<stdio.h>//header
file
#include<conio.h>
/* Deklarasi struct */
typedef struct Node{
int data; //data pada tree
Node *kiri; //penunjuk node anak kiri
Node *kanan; //penunjuk node anak kanan
};
/* Fungsi untuk
memasukkan data ke dalam tree */
void tambah(Node
**root, int databaru){
if((*root) == NULL){ //jika
pohon/subpohon masih kosong
Node *baru;//node “baru” dibentuk…
baru = new Node;//berdasarkan struct “Node”
baru->data = databaru; //data node baru diisi oleh variabel databaru
baru->kiri = NULL;//penunjuk kiri node baru masih kosong
baru->kanan = NULL;//penunjuk kanan node baru masih kosong
(*root) = baru; //node pohon (root) diletakkan pada node baru
(*root)->kiri = NULL;//penunjuk kiri node root masih kosong
(*root)->kanan = NULL; //penunjuk kanan node root masih kosong
printf(“Data bertambah!”);
}
else if(databaru < (*root)->data)//jika databaru kurang dari data node
root…
tambah(&(*root)->kiri, databaru);//tambahkan databaru pada subpohon
kiri
else if(databaru > (*root)->data)//jika databaru lebih dari data node
root…
tambah(&(*root)->kanan, databaru); //tambahkan databaru pada subpohon
kanan
else if(databaru == (*root)->data)//jika databaru sama dengan data node
root
printf(“Data sudah ada!”);//databaru tidak dapat ditambahkan pada tree
}
/* Fungsi untuk
menampilkan data secara pre-order
(data
ditampilkan dari node induk, node anak kiri, lalu node anak kanan)
*/
void preOrder(Node
*root){
if(root != NULL){//jika pohon/subpohon tidak kosong
printf(“%d “, root->data);//menampilkan data node yang dikunjungi
preOrder(root->kiri);//mengunjungi node anak kiri
preOrder(root->kanan); //mengunjungi node anak kanan
}
}
/* Fungsi untuk
menampilkan data secara in-order
(data
ditampilkan dari node anak kiri, node induk, lalu node anak kanan)
*/
void inOrder(Node
*root){
if(root != NULL){//jika pohon/subpohon tidak kosong…
inOrder(root->kiri);//mengunjungi node anak kiri
printf(“%d “, root->data);//menampilkan data node yang dikunjungi
inOrder(root->kanan);//mengunjungi node anak kanan
}
}
/* Fungsi untuk
menampilkan data secara post-order
(data
ditampilkan dari node anak kiri, node anak kanan, lalu node induk)
*/
void postOrder(Node
*root){
if(root != NULL){//jika pohon/subpohon tidak kosong
postOrder(root->kiri); //mengunjungi node anak kiri
postOrder(root->kanan);//mengunjungi node anak kanan
printf(“%d “, root->data); //menampilkan data node yang dikunjungi
}
}
main(){
int pil, c;
Node *pohon, *t;
pohon = NULL;
do{
int data;
printf(“MENU\n”);
printf(“1. Tambah\n”);
printf(“2. Lihat Pre-Order\n”);
printf(“3. Lihat In-Order\n”);
printf(“4. Lihat Post-Order\n”);
printf(“5. Exit\n”);
printf(“Pilihan : “); scanf(“%d”, &pil);
switch(pil){
case 1 :
printf(“Data baru : “);
scanf(“%d”, &data);
tambah(&pohon, data);
break;
case 2 :
if(pohon != NULL)
preOrder(pohon);
else
printf(“Masih kosong!”);
break;
case 3 :
if(pohon != NULL)
inOrder(pohon);
else
printf(“Masih
kosong!”);
break;
case 4 :
if(pohon != NULL)
postOrder(pohon);
else
printf(“Masih kosong!”);
break;
}
getch();
printf(“\n”);
}
while(pil != 5);
}
|
Hasil:

2.
PENGERTIAN GRAPH
Graph
adalah himpunan verteks dan himpunan sisi (edge). keterhubungan antara verteks.
Biasanya untuk suatu graph G digunakan notasi matematis. Verteks menyatakan
entitas-entitas data dan sisi menyatakan G = (V, E) Dimana :
G=
Graph
V=
Simpul atau Vartex, atau Node, atau Titik
E=
Busur atau Edge, atau Edge, atau arc
V
adalah himpunan verteks dan E himpunan sisi yang terdefinisi antara
pasangan-pasangan verteks. Sebuah sisi antara verteks x dan y ditulis {x,y}.
Suatu graph H = (V1, E1) disebut subgraph dari graph G jika V1 adalah himpunan
bagian dari V dan E1 himpunan bagian dari E. Cara pendefinisian lain untuk
graph adalah dengan menggunakan himpunan keterhubungan langsung Vx. Pada setiap
verteks x terdefinisi Vx sebagai himpunan dari verteks-verteks yang adjacent
dari. Dalam digraph didefinisikan juga terminologi-terminologi
berikut ini.Predesesor dari suatu verteks x (ditulis Pred(x)) adalah himpunan
semua vertex yang adjacent ke x. Suksesor dari verteks x (ditulis Succ(x))
adalah himpunan. Struktur data bergantung pada struktur graph dan algoritma
yang digunakan untuk memmanipulasi graph. Secara teori salah satu dari keduanya
dapat dibedakan antara struktur list dan matriks, tetapi dalam penggunaannya
struktur terbaik yang sering digunakan adalah kombinasi keduanya.
Kemudian
terdapat istilah-istilah yang berkaitan dengan graph yaitu:
1. Vertex Adalah himpunan node / titik pada sebuah
graph.
2. Edge Adalah himpunan garis yang menghubungkan
tiap node / vertex
3. Adjacent Adalah dua buah titik dikatakan
berdekatan (adjacent) jika dua buah titik tersebut terhubung dengan sebuah
sisi. Adalah Sisi e3 = v2v3 insident dengan titik v2 dan titik v3, tetapi sisi
e3 = v2v3 tidak insident dengan titik v1 dan titik v4. Titik v1 adjacent dengan
titik v2 dan titik v3, tetapi titik v1 tidak adjacent dengan titik v4.
4. Weight Adalah Sebuah graf G = (V, E) disebut
sebuah graf berbobot (weight graph), apabila terdapat sebuah fungsi bobot
bernilai real W pada himpunan E, nilai W (e) disebut bobot untuk sisi e, "
e Î E. Graf berbobot tersebut dinyatakan pula sebagai G = (V, E, W).
5. Path Adalah Walk dengan setiap vertex berbeda.
Contoh, P = D5B4C2A Sebuah walk (W) didefinisikan sebagai urutan (tdk nol)
vertex & edge. Diawali origin vertex dan diakhiri terminus vertex. Dan
setiap 2 edge berurutan adalah series. Contoh, W = A1B3C4B1A2.
6. Cycle Adalah Siklus (Cycle) atau Sirkuit
(Circuit) Lintasan yang berawal dan berakhir pada simpul yang sama.
Komentar
Posting Komentar